Geometric Solids

---

Go to Plato's Five Regular Polyhedra and Archimedean Polyhedra

MATERIAL:

PURPOSE:

1) A study of the classification of geometric solids as a foundation

for the later study of geometry.

 

2) To learn the words which will be needed and which will allow the

child to express himself.

 

3) To make the child aware of solid forms in the environment and to

get him to observe the environment with intelligence.

PRESENTATION:

Place the five Platonian solids in the classroom together for the

children to handle. The children must be able to hold the solids

in their hands.

 

Later, after the children have handled the solids and are familiar

with them, introduce the terminology associated with the Platonian

solids.

 

Polyhedron and polyhedra (plural) means many faces.

 

Apex and apices or apexes (plural) - the vertex of an angle. A

solid is regular if the spices are the same.

 

Polyhedra have a face, edge, and apex. The Platonian solids were

first described by Plato.

 

There are nine regular solids: the five Platonian, pictured above, and the four polyhedra described by Kepler-Poinsot. Each face, apex and angle on each respective solid is the same.

Platonian solids:

1. Tetrahedron - 4 faces, each face an equilateral triangle

2. Hexahedron - 6 faces, each face is a square

3. Octahedron - 8 faces, each face is an equilateral triangle

4. Dodecahedron - 12 faces, each face is a pentagon (5 edges)

5. Icosahedron - 20 faces, each face is an equilateral triangle

 

Kepler-Poinsot solids: four star shaped regular polyhedra; three were

described by Kepler and one by Poinsot. The teacher should at least present a picture of these 4 solids to the children.

 

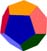
Semi-regular polyhedra: These have faces of more than one shape. Thirteen

semi-regular polyhedra were described by Archimedes. Present at least a picture of them so the children can see them.

Solids Bounded by Straight Lines:

Prisms:

The end face can be any regular polygon.

The sides are always rectangles.

Prisms are named by their end faces. For example, the triangular prism has triangles

as end faces, and the hexagonal prism has hexagons as the end faces.

 

Pyramids:

These have any regular polygon for a base and isosceles triangles with a common vertex as the sides.

A pyramid is named by its base (hexagonal pyramid, etc.).

Regular Curved Solids:

Sphere: all points on the surface are equidistant from the center

Ellipsoid: a form whose plane surfaces are either ellipses or circles

Ovoid: egg shaped

Torus: a rounded form on a circular base in the case of a circle, resembling a doughnut

 

When the children handle these, let them also roll them and watch

the path each takes.

Curved solids with plane and curved surfaces

Cylinder: a solid bounded by two parallel planes which are curved

Cone: a solid with a circular base joined by straight lines to the vertex

Hemisphere: half a sphere

Plato's Five Regular Polyhedra

TETRAHEDRON

HEXAHEDRON

OCTAHEDRON

DODECAHEDRON

ICOSAHEDRON

Archimedian Polyhedra

TRUNCATED TETRAHEDRON

TRUNCATED CUBE

TRUNCATED OCTAHEDRON

SNUB CUBE

TRUNCATED OCTAHEDRON

TRUNCATED ICOSAHEDRON

SMALL RHOMBICUBOCHEDRON

GREAT RHOMBECUBOCTAHEDRON

CUBOCTAHEDRON

ICOSIDODECAHEDRON

SNUB DODECAHEDRON

SMALL RHOMBICOSIDODECAHEDRON

Home Page | Readings and Reference

Table of Contents